Come utilizzare la sezione aurea
Vi è mai successo di comporre un elaborato grafico, logo o pagina web, e avere la sensazione che qualcosa non quadri?
Succede di avvertire una irregolarità, qualcosa che non funziona, e non riuscire a capire cosa sia.
Quando manca equilibrio il nostro cervello percepisce la disarmonia, ma senza conoscenze tecniche non è possibile superare l’ostacolo. Chiunque guarderà la nostra composizione avrà la stessa sensazione, e solo conoscendo il concetto di sezione aurea è possibile riportare l’equilibrio.
Definizione matematica di constante aurea
Euclide la chiamava la “divina proporzione” ed è stata utilizzata dai più grandi artisti dei secoli passati, come Leonardo e Mozart, e da alcuni studi risulta nota già ai tempi dei fenici.
La proporzione aurea, nota in matematica come Phi o costante di Fidia, è una costante del valore di 1,6180339887 (e molti altri decimali). È calcolata con le lunghezze di due segmenti messi in rapporto tra loro.
Φ = 1,6180339887498 …..
Si calcola così:
presi due segmenti A e B, con A maggiore di B, il rapporto tra A e B è uguale al rapporto tra la loro somma (A+B) e il segmento più lungo.
se immaginiamo che il segmento A misura 1 cm e B 0,618 cm, possiamo riscrivere la formula:
A:B= (A+B):A cioè 1:0,618 = (1+0,618):1
Questa proporzione tra le dimensioni di una forma dona armonia ed equilibrio. I principali loghi di successo, per esempio quello di national geografic, seguono questa regola.

Chi è Fibonacci?
Il numero Φ e la sezione aurea si intrecciano con un altro concetto matematico: la serie di Fibonacci. È una successione di numeri dei quali ogni membro è la somma dei due precedenti.
0, 1, 1, 2, 3, 5, 8, 13 …
Se si fa il rapporto tra un numero qualunque della serie e il precedente si ottiene un risultato che si avvicina (o in eccesso o in difetto) sempre più a Φ, man mano che si procede con i termini situati più avanti nella serie.
Leonardo Fibonacci era un matematico pisano del XII secolo ed elaborò la sua nota teoria partecipando ad un gara fra matematici indetta dall’imperatore Federico II che propose un singolare e, all’apparenza, banale quesito:
si rinchiude una coppia di conigli in un recinto: quante coppie di conigli si ottengono in un anno supponendo che ogni coppia dia alla luce un’altra coppia ogni mese, che le coppie più giovani siano in grado di riprodursi dal secondo mese di vita e che la coppia non muore mai?
Fibonacci ragionò così: all’inizio c’è solo una coppia di conigli, il primo mese ce ne sono 2 di cui una fertile, il secondo ce ne sono 3 di cui 2 fertili, il terzo mese ce ne sono 5 di cui 3 fertili, il quarto mese ce ne sono 8 di cui 5 fertili e così via. Notò che ogni termine della sequenza è la somma dei due precedenti.
Ecco spiegata la serie di Fibonacci
L’argomento potrebbe essere approfondito molto di più, ci sarebbero dimostrazioni matematiche interessanti da vedere, ma preferisco lasciare al lettore la scelta di proseguire.
Lascio qui sotto il link di wikipedia
Cos’è una sezione aurea e come si costruisce?
vediamo come la serie di Fibonacci ci aiuta a costruire la sezione aurea e ci guida nelle composizioni visive.
Seguendo la serie di Fibonacci è possibile costruire un rettangolo aureo e su di esso modellare una spirale aurea.
Da questo schema nascono diverse varianti che possono essere utilizzate in tutte le composizioni visive, sia per la fotografia sia per l’impaginazione grafica.
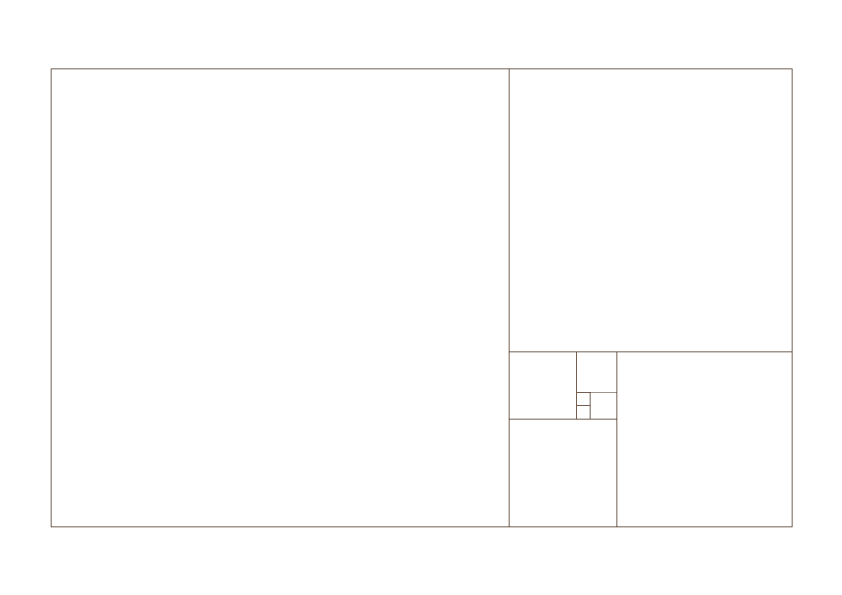
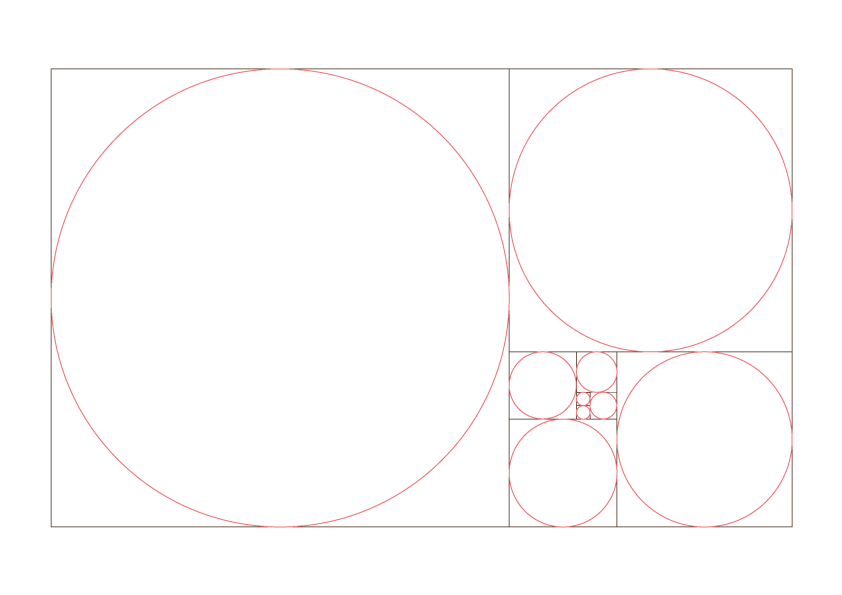
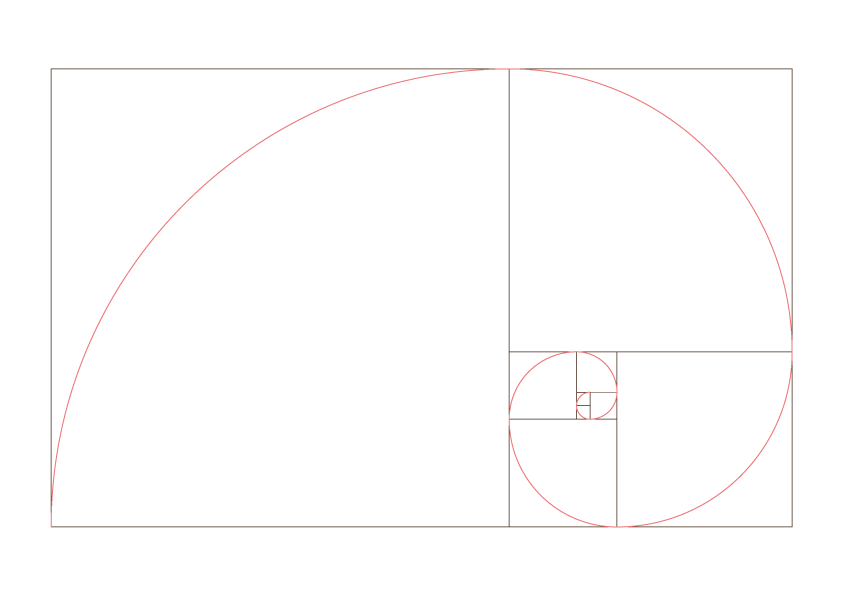
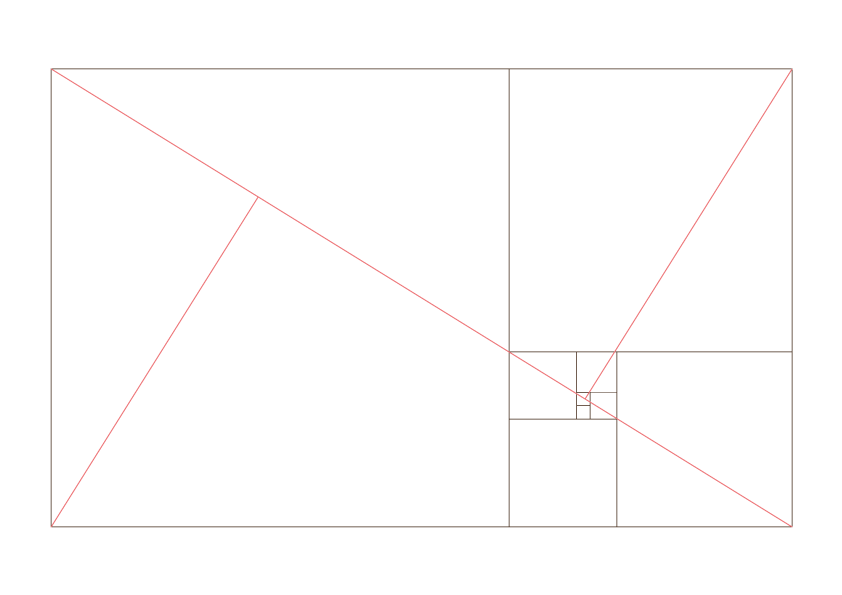
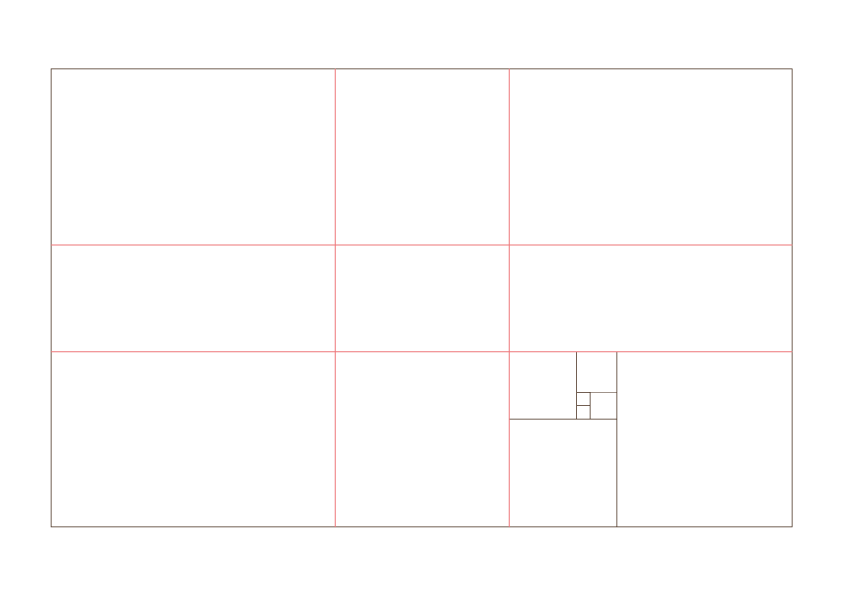
Esempi di utilizzo





La sezione aurea nei loghi noti
Questi sono alcuni esempi di come le sezione aurea è stata utilizzata per comporre loghi noti:
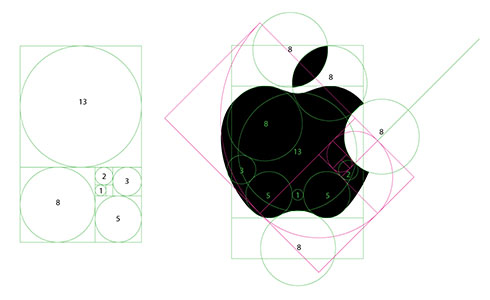


Come utilizzare la sezione aurea nella costruzione di un logo
Utilizzando la costante aurea, è possibile determinare il rapporto tra le dimensioni di un logo.
Vediamo degli esempi:
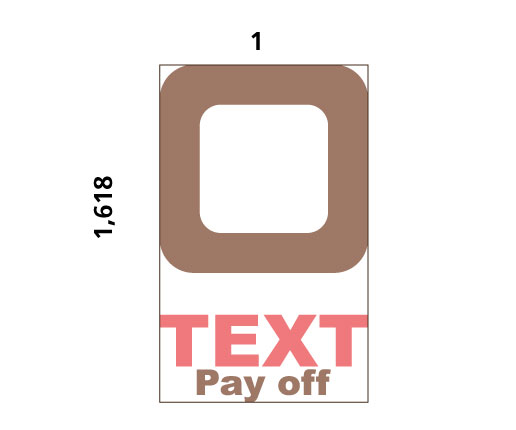
Rapporto tra testo e pay off

Rapporto tra pittogramma e testo
con sviluppo orizzontale

Rapporto tra pittogramma e testo
con sviluppo verticale

Rapporto tra gli elementi del pittogramma

Sviluppo del logo in un rettangolo aureo
Se l’articolo ti è piaciuto, lascia un commento.
Qui sotto trovi anche i tasti per mandarmi una mail o seguirmi su Instagram!








